Read. Observe. Learn. :-) DCW Endeavors

How the JS Solid Cube Works

A piece by piece deconstruction of the code behind dionyziz's rotating solid cube.

Posted by DCW on 05-12-2022 9:23 PM

This blog post discusses the programming code behind the rotating solid cube by dionyziz.

I want to preface this blog by stating a few things. First, this program is not as complicated as it might seem. And secondly, most of the code is simply the use of for loops, a Vector class, and other code to organize points for triangle shapes. The triangle shapes make the sides of the cube. But it is how the triangle shapes are created and stored before being rendered that can get a bit difficult to understand. However once the triangles are ready to be rendered, it's simply the use of rotation functions, x/z+view_distance or y/z+view_distance calculations, and cross product calculations to determine if z is a positive number so it can be viewed (the positive z-axis points toward your eye).

For this discussion I will be using a test file named solidcube.html. I wanted to keep things simple because the file that displays the solid cube on my website has other code beyond the scope of this blog post (and would make things even more confusing and I wanted to avoid that :-)).

The solid cube program consists of three files:

  1. solidcube.html – displays the solid cube on html canvas, within an html page.
  2. cube2_2.js – contains the main functions to run, display, and move the solid cube (note - this file has been named as such to distinguish it from other similar files in my folder).
  3. vector.js – contains the code for a Vector class.

The main file, and like I mentioned a test file, has very simple code - a title for the web page, a refresh program button (and associated brief js code) and a html canvas for the rotating cube itself. (also included, but not shown, are bootstrap links between the head tags)

<!DOCTYPE html>
<html lang="en">
<head><title>solidcube.html</title>
<script>
function reloadProgram(){
if(confirm("Reload cube program? Click OK to proceed or else click cancel.")){
location.reload();
}
}
</script>
</head>
<body>
<h4 style="text-align:center; padding-top:10px;">solidcube.html</h4>
<p style="text-align:center;">
<button onclick="reloadProgram();">Reload Cube Program</button>
</p>
<div class="container text-center">
<canvas id="canvas" width="600" height="600" style="border-radius: 5px;"></canvas>
</div>

<script src="js/vector.js"></script>
<script src="js/cube2_2.js"></script>

</body>
</html>

A side note - the above html code was formatted for display on this web page by the awesome HTML escape.net website.

Below is a screen shot of solidcube.html:

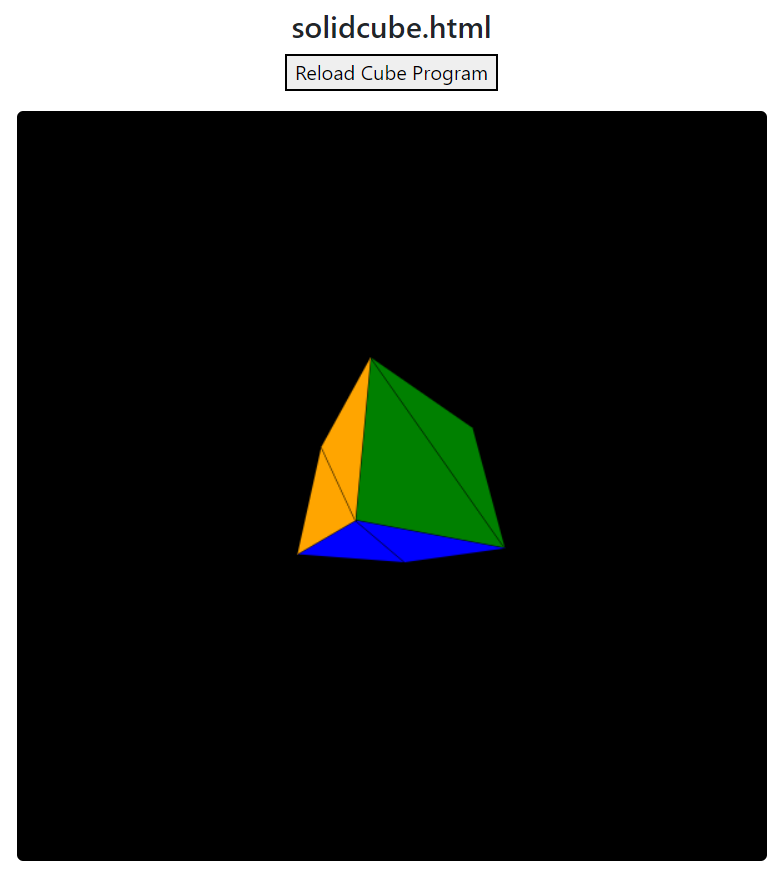
In cube2_2.js there are some global variables listed at the top of the file. 


var W = 600, H = 600; //variables for size of canvas
//var STEP = 0.3;//original one is 0.5 - ALSO NOT BEING USED NOW
//var perspective_distance = 3.5;//was 2.5 - ALSO NOT BEING USED NOW
var MODEL_MIN_X = -2, MODEL_MAX_X = 2;
var MODEL_MIN_Y = -2, MODEL_MAX_Y = 2;
var canvas = document.getElementById('canvas');
var ctx = canvas.getContext('2d');
//view_distance - lower numbers closer, higher numbers farther away
var view_distance = 3; //used in perspectiveProjection(point), original is 4 - and larger number draws cube farther away

//angle values:
var theta = 0.5;//original value was 0
var dtheta = 0.01;//original value was 0.01 - note, 0.2 makes the cube spin rapidly
var background_color = 'black';
var angle_mult = 0.5;//original value 0.43 - appears to control if top of cube is shown during the rotation process

var points = []; //points array instantiation
var triangles = [];//triangle array to create sides of the box object
var colors = [//original amount was 6 colors - have 12 now to color each triangle
    'red', 'green', 'blue', 'white', 
    'orange', 'purple', 'cyan', 'yellow',
	'pink', 'tan', 'palevioletred', 'olive'
];

I will discuss the code in cube2_2.js in the order that it is called.

Upon first loading the web page, two functions are called in this order:

  1. initGeometry();
  2. render();

initGeometry();//called first
render(); //then this function is called

FIRST SECTION OF THE PROGRAM – initGeometry()

So let’s take a look at initGeometry() first. Here is the code for this function (along with some helpful comments): 


//Function to create square sides using triangles 
//Start at dimension 0 and go up to dimension 2
/*
a.
dimension 0 is x
dimension 1 is y
dimension 2 is z
++dimension explanation:
++x (pre-increment) 
if x = 0;
y = array[x++]; // This will get array[0]
x++ (post-increment) 
x = 0;
y = array[++x]; // This will get array[1]
b. side means that for x, y, and z each direction has a -1 part and a 1 part, and +=2 will make sure each one covered
c. points is that each side will have the points done to 
make 2 triangles per side face 
*/
function initGeometry(){
  //cube is only going to have -1 and 1 for each side, 
  //doesnt' need all the points like in point cube, his first video
    for(var x = -1; x <= 1; x +=2){
	  for(var y = -1; y <= 1; y +=2){
	    for(var z = -1; z <= 1; z +=2){
		  //NOTE - Vector is a class in vector.js file
          points.push(new Vector(x,y,z));
		}
	  }
	}
	//NOTE - THIS 'for' loop below is what gets 
	//points for both neg and pos sides of cube along each axis
	for(var dimension = 0; dimension <= 2; ++dimension){
	  for(var side = -1; side <= 1; side += 2){
	    var sidePoints = points.filter((point) => {
				
		return point[dimension] == side;//return if point[dimension] is equal to side 
		//(but return is meant to return a value to sidePoints 
		//from points.filter() keep in mind, 
		//it does not return out of the current for loop or initGeometry())
		});
			
	var a = sidePoints[0], 
		b = sidePoints[1],
		c = sidePoints[2],
		d = sidePoints[3];
		//console.log("a = "+a.print()+" b = "+b.print()+" c = "+c.print()+" d = "+d.print());
            
        if(dimension == 1){/*he added this due to issues with y dimension, around 35:00 mark in video*/
				
		  triangles.push(makeTriangle(a,b,c,dimension,side));
		  triangles.push(makeTriangle(d,b,c,dimension,side));
        }else{
          triangles.push(makeTriangle(a,b,c,dimension,-side));
          triangles.push(makeTriangle(d,b,c,dimension,-side));//he said adding -side was needed because he made an error in his crossproduct function
        }
     }//end for loop for side
   }//end for loop for dimension
}

Recall that there is a points array listed in the global variables. 


var points = []; //points array instantiation

First, the for loop fills the points array.


for(var x = -1; x <= 1; x +=2){
   for(var y = -1; y <= 1; y +=2){
      for(var z = -1; z <= 1; z +=2){
      //NOTE - Vector is a class in vector.js file
       points.push(new Vector(x,y,z));
      }
    }
}

As mentioned in the JavaScript comments, each x, y, and z 3D point below is one of the eight corners of the cube.

x = -1 y = -1 x = -1
x = -1 y = -1 x = 1
x = -1 y = 1 x = -1
x = -1 y = 1 x = 1
x = 1 y = -1 x = -1
x = 1 y = -1 x = 1
x = 1 y = 1 x = -1
x = 1 y = 1 x = 1

Each of the eight 3D corner points is put into the points array as an instantiation of the Vector class. The JavaScript array function push() helps to accomplish this by placing a new item into the points array. 


points.push(new Vector(x,y,z));

Here is the constructor for the Vector class. The new Vector(x, y, z) portion of the code produces a 3 value array placed into the points array. For example, the first row of the table, this[0] = -1, this[1] = -1, and this[2] = -1, is “pushed” into points[0]. 


class Vector{
    constructor(x,y,z){
        this[0] = x;
        this[1] = y;
        this[2] = z;
        
    }

With the next code section of initGeometry() there is another important for loop. I placed some console.log() functions in various locations within this for loop to gather a better understanding of the code. To learn more about viewing console.log() outputs see this link. 


//NOTE - THIS for loop below is what gets points for both neg and pos sides of cube along each axis
	for(var dimension = 0; dimension <= 2; ++dimension){
	  for(var side = -1; side <= 1; side += 2){
	    //NOTE - filter is a js function for arrays
		//console.log("dimension = "+dimension+" side = "+side);
		var sidePoints = points.filter((point) => {
		  return point[dimension] == side;//return if point[dimension] is equal to side 
		//(but return is meant to return a value to sidePoints 
		//from points.filter() keep in mind, 
		//it does not return out of the current for loop or initGeometry())
		});
	//console.log("points["+dimension+"] = "+points[dimension]);
	//console.log("sidePoints["+dimension+"] = "+sidePoints[dimension]);
	var a = sidePoints[0], 
		b = sidePoints[1],
		c = sidePoints[2],
		d = sidePoints[3];
		//console.log("a = "+a.print()+" b = "+b.print()+" c = "+c.print()+" d = "+d.print());
            
        if(dimension == 1){//he added this due to issues with y dimension, around 35:00 mark in video
				
		  triangles.push(makeTriangle(a,b,c,dimension,side));
		  triangles.push(makeTriangle(d,b,c,dimension,side));
        }else{
          triangles.push(makeTriangle(a,b,c,dimension,-side));
          triangles.push(makeTriangle(d,b,c,dimension,-side));//he said adding -side was needed because he made an error in his crossproduct function
        }
	  }//end for loop for side
	}//end for loop for dimension

Note that the function sidePoints = points.filter((point) => { return point[dimension] == side;} uses the arrow function => . This is explained in more detail in the 2nd section of this blog. However, to learn more now, click this link

After analyzing the console.log() messages, I could see more clearly what was occurring with the code. I placed an asterisk wherever point[dimension] == side is true, and is therefore returned to sidePoints. Also, I added a print() function to the Vector class that prints this[n] of each vector instantiation, though later in this blog I changed print() to only having the number itself printed.

dimension = 0 side = -1
*point[0] = -1 side = -1 //point[0] = -1
point[0] = 1 side = -1
a = this[0] = -1 this[1] = -1 this[2] = -1
b = this[0] = -1 this[1] = -1 this[2] = 1
c = this[0] = -1 this[1] = 1 this[2] = -1
d = this[0] = -1 this[1] = 1 this[2] = 1 		dimension = 0 side = 1
point[0] = -1 side = 1
*point[0] = 1 side = 1 //point[0] = 1
a = this[0] = 1 this[1] = -1 this[2] = -1
b = this[0] = 1 this[1] = -1 this[2] = 1
c = this[0] = 1 this[1] = 1 this[2] = -1
d = this[0] = 1 this[1] = 1 this[2] = 1
dimension = 1 side = -1
*point[1] = -1 side = -1 //point[1] = -1
point[1] = 1 side = -1
*point[1] = -1 side = -1
point[1] = 1 side = -1
a = this[0] = -1 this[1] = -1 this[2] = -1
b = this[0] = -1 this[1] = -1 this[2] = 1
c = this[0] = 1 this[1] = -1 this[2] = -1
d = this[0] = 1 this[1] = -1 this[2] = 1 		dimension = 1 side = 1
point[1] = -1 side = 1
*point[1] = 1 side = 1 //point[1] = 1
point[1] = -1 side = 1
*point[1] = 1 side = 1
a = this[0] = -1 this[1] = 1 this[2] = -1
b = this[0] = -1 this[1] = 1 this[2] = 1
c = this[0] = 1 this[1] = 1 this[2] = -1
d = this[0] = 1 this[1] = 1 this[2] = 1
dimension = 2 side = -1
*point[2] = -1 side = -1
point[2] = 1 side = -1
*point[2] = -1 side = -1 //point[2] = -1
point[2] = 1 side = -1
*point[2] = -1 side = -1
point[2] = 1 side = -1
*point[2] = -1 side = -1
point[2] = 1 side = -1
a = this[0] = -1 this[1] = -1 this[2] = -1
b = this[0] = -1 this[1] = 1 this[2] = -1
c = this[0] = 1 this[1] = -1 this[2] = -1
d = this[0] = 1 this[1] = 1 this[2] = -1 		dimension = 2 side = 1
point[2] = -1 side = 1
*point[2] = 1 side = 1 //point[2] = 1
point[2] = -1 side = 1
*point[2] = 1 side = 1
point[2] = -1 side = 1
*point[2] = 1 side = 1
point[2] = -1 side = 1
*point[2] = 1 side = 1
a = this[0] = -1 this[1] = -1 this[2] = 1
b = this[0] = -1 this[1] = 1 this[2] = 1
c = this[0] = 1 this[1] = -1 this[2] = 1
d = this[0] = 1 this[1] = 1 this[2] = 1

There are six sides to a cube. What the code does from the start of the first for loop until the if(dimension == 1) part is create a, b, c and d, which each hold 3 numbers for the corners of the cube.

And if you notice, each grouping of a, b, c, and d together form each particular side of the cube. See the sketch below to help visualize this.

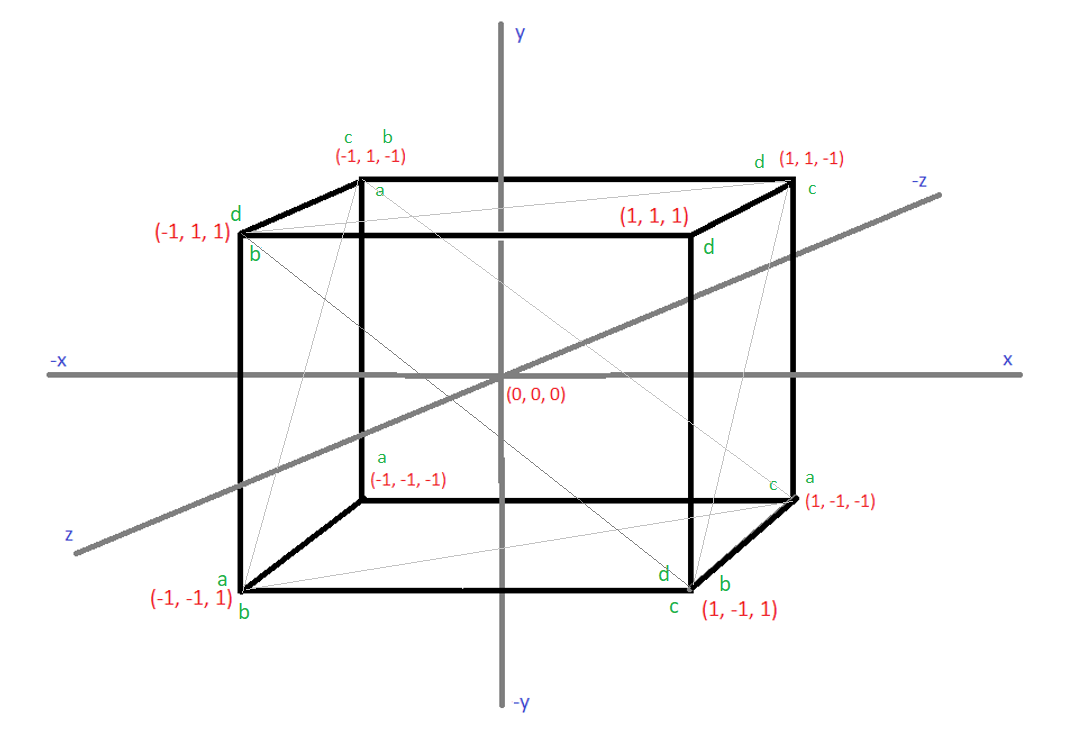
As explained in dionyziz's video and as I typed in my beginning comments for the program, the details below are probably apparent now:

dimension 0 is x.
side -1 is negative x side.
side 1 is positive x side.

dimension 1 is y.
side -1 is negative y side.
side 1 is positive y side.

dimension 2 is z.
side -1 is negative z side.
side 1 is positive z side.

For example, let's take a look at one side of the cube, dimension 0, which is the x axis, and side -1, which is the negative side of the x axis. Here are the four corners of the negative x side of the cube (view the cube sketch above to confirm this):

a = (-1, -1, -1)

b = (-1, -1, -1)

c = (-1, -1, -1)

d = (-1, -1, -1)

And so it is for the remaining five sides, with each side categorized by its dimension number and side number.

At the end of the for loop is an if-else statement. As can be seen by my comments (which I added while typing down the code from dionyziz’s video) some errors occurred while he was working on the program. He made the if-else to adjust for the errors. He is adjusting for dimension 1, the y axis. After going over his code, I am still not sure of the specific error, but I do know his Vector class cross product differs from the usual cross product - I'll explain that more a little later. 


if(dimension == 1){//he added this due to issues with y dimension, around 35:00 mark in video		
    triangles.push(makeTriangle(a,b,c,dimension,side));
	triangles.push(makeTriangle(d,b,c,dimension,side));
}else{
    triangles.push(makeTriangle(a,b,c,dimension,-side));
    triangles.push(makeTriangle(d,b,c,dimension,-side));//he said adding -side was needed 
	//because he made an error in his crossproduct function
}

Also, notice he added a -side in the else section, as a parameter in makeTriangle().

Here is what is basically happening in this section of the code. The array triangles[ ], one of the global variables at the top of cube2_2.js will be getting the necessary points to create a triangle. 


triangles.push(makeTriangle(a,b,c,dimension,side));
triangles.push(makeTriangle(d,b,c,dimension,side));

OR


triangles.push(makeTriangle(a,b,c,dimension,-side));
triangles.push(makeTriangle(d,b,c,dimension,-side));

The function makeTriangle() will produce three sets of 3 points each to be placed in the triangles array by using the JavaScript array function push(). You can learn more about the push() function here. Note that the makeTriangle() function is called twice per if or else section. The function is called twice so as to create the two triangles per cube side.

To help make things a little clearer, I placed console.log() functions within initGeometry() and the makeTriangle() function (also between the '//test code below - needs to be removed' and '//end test code') to get some helpful output. Again, here is a link to learn more about console.log() at the w3schools web page. 


function makeTriangle(a,b,c,dimension,side){
    var side1 = b.subtract(a),
        side2 = c.subtract(a);
	//console.log("side1 = "+side1.print()+" side2 = "+side2.print());
    var orientationVector = side1.cross(side2);
	
	//test code below - needs to be removed
	//console.log("orientationVector = "+orientationVector.print());
	var testcross1 = Math.sign(orientationVector[dimension]);
	var testcross2 = Math.sign(side);
	//console.log("Math.sign(orientationVector["+dimension+"]) = "+testcross1+" Math.sign(side) = "+testcross2);
	//end test code

    if(Math.sign(orientationVector[dimension]) == Math.sign(side)){
		//console.log("return a,b,c "+a.print()+", "+b.print()+", "+c.print());
        return [a,b,c];
    }
	//console.log("return a,c,b "+a.print()+", "+c.print()+", "+b.print());
    return [a,c,b];
}

And here is the output from those console.log() functions:

dimension = 0 side = -1 //neg x side
side1 = (0, 0, 2) side2 = (0, 2, 0)
orientationVector = (-4, 0, 0)
Math.sign(orientationVector[0]) = -1 Math.sign(side) = 1
return a,c,b (-1, -1, -1), (-1, 1, -1), (-1, -1, 1)
side1 = (0, -2, 0) side2 = (0, 0, -2)
orientationVector = (4, 0, 0)
Math.sign(orientationVector[0]) = 1 Math.sign(side) = 1
return a,b,c (-1, 1, 1), (-1, -1, 1), (-1, 1, -1) 		dimension = 0 side = 1 //pos x side
side1 = (0, 0, 2) side2 = (0, 2, 0)
orientationVector = (-4, 0, 0)
Math.sign(orientationVector[0]) = -1 Math.sign(side) = -1
return a,b,c (1, -1, -1), (1, -1, 1), (1, 1, -1)
side1 = (0, -2, 0) side2 = (0, 0, -2)
orientationVector = (4, 0, 0)
Math.sign(orientationVector[0]) = 1 Math.sign(side) = -1
return a,c,b (1, 1, 1), (1, 1, -1), (1, -1, 1)
dimension = 1 side = -1 //neg y side
side1 = (0, 0, 2) side2 = (2, 0, 0)
orientationVector = (0, -4, 0)
Math.sign(orientationVector[1]) = -1 Math.sign(side) = -1
return a,b,c (-1, -1, -1), (-1, -1, 1), (1, -1, -1)
side1 = (-2, 0, 0) side2 = (0, 0, -2)
orientationVector = (0, 4, 0)
Math.sign(orientationVector[1]) = 1 Math.sign(side) = -1
return a,c,b (1, -1, 1), (1, -1, -1), (-1, -1, 1) 		dimension = 1 side = 1 //pos y side
side1 = (0, 0, 2) side2 = (2, 0, 0)
orientationVector = (0, -4, 0)
Math.sign(orientationVector[1]) = -1 Math.sign(side) = 1
return a,c,b (-1, 1, -1), (1, 1, -1), (-1, 1, 1)
side1 = (-2, 0, 0) side2 = (0, 0, -2)
orientationVector = (0, 4, 0)
Math.sign(orientationVector[1]) = 1 Math.sign(side) = 1
return a,b,c (1, 1, 1), (-1, 1, 1), (1, 1, -1)
dimension = 2 side = -1 //neg z side
side1 = (0, 2, 0) side2 = (2, 0, 0)
orientationVector = (0, 0, -4)
Math.sign(orientationVector[2]) = -1 Math.sign(side) = 1
return a,c,b (-1, -1, -1), (1, -1, -1), (-1, 1, -1)
side1 = (-2, 0, 0) side2 = (0, -2, 0)
orientationVector = (0, 0, 4)
Math.sign(orientationVector[2]) = 1 Math.sign(side) = 1
return a,b,c (1, 1, -1), (-1, 1, -1), (1, -1, -1) 		dimension = 2 side = 1 //pos z side
side1 = (0, 2, 0) side2 = (2, 0, 0)
orientationVector = (0, 0, -4)
Math.sign(orientationVector[2]) = -1 Math.sign(side) = -1
return a,b,c (-1, -1, 1), (-1, 1, 1), (1, -1, 1)
side1 = (-2, 0, 0) side2 = (0, -2, 0)
orientationVector = (0, 0, 4)
Math.sign(orientationVector[2]) = 1 Math.sign(side) = -1
return a,c,b (1, 1, 1), (1, -1, 1), (-1, 1, 1)

Okay. I will explain some more details. First, examine the code below. The subtract() function and cross() function are both present in the Vector class file, vector.js. 


var side1 = b.subtract(a),
    side2 = c.subtract(a);
var orientationVector = side1.cross(side2);

By subtracting the points at b - a and c - a this will give two vectors, side1 and side2 respectively, that can then be used by the cross function. The cross function calculates the cross product of two vectors. Note that I gave as a comment the cross product calculation that I used in my matrix vector 2D 3D graphing calculator . This is the typical means to calculate a cross product. dionyziz did his cross product calculation differently. 


/*//from my cross product on 3d graphing 
vx = y1*z2 - z1*y2;
vy = z1*x2 - x1*z2;
vz = x1*y2 - y1*x2;
*/
    
cross(other){
   return new Vector(
     this[1] * other[2] - this[2] * other[1],
     this[0] * other[2] - this[2] * other[0],
	//this[2]*other[0] - this[0]*other[2],
     this[0] * other[1] - this[1] * other[0]
   );
}
    
//this function determines if orientation is clockwise or counterclockwise for figuring out if camera (our eye) can see triangle or not
ccw(other){
   return this.cross(other)[2] > 0; //checks to see if z is positive or not, because if its negative, we cannot see it then
}

But regardless, note the console.log() output:
dimension = 0 side = -1 //neg x side
side1 = (0, 0, 2) side2 = (0, 2, 0)
orientationVector = (-4, 0, 0)
and side1 = (0, -2, 0) side2 = (0, 0, -2)
orientationVector = (4, 0, 0)

Recall makeTriangle() is called twice but with a,b,c and then with d,b,c:


triangles.push(makeTriangle(a,b,c,dimension,side));
triangles.push(makeTriangle(d,b,c,dimension,side));
So, when a,b,c is inputted, for dimension 0 (x axis) side -1 (neg. x axis side) the cross product of vector side1 and vector side2 is the orientationVector (-4, 0, 0). And then next time when d,b,c is inputted, the orientationVector will be (4, 0, 0).

This is simply dionyziz's means to distinguish both triangles so they can then be passed on to more program code to eventually be drawn on the canvas. He could have done this differently. He simply could have created an array with all the points already established, like (-1,-1,-1), (-1,1,-1) etc. and then combined them with certain code, but honestly his way is quite ingenious and awesome. I'm impressed :-)

This will conclude the discussion of the code within initGeometry().

SECOND SECTION OF THE PROGRAM – render()

In function render() the actual drawing of the canvas and the cube is accomplished.


function render(){
	ctx.fillStyle = background_color;//was black
	ctx.fillRect(0,0,W,H);
	theta += dtheta;
	/*
	Each triangle is altered by forEach
	Each point for each triangle then has its points rotated by rotateY() and rotateX. Both those functions reside within the vector.js class
	Also, the => symbol is used.
	example: 
		let myFunction = (a, b) => a * b;
		document.getElementById("demo").innerHTML = myFunction(4, 5);
		answer: 20
	Syntax:
	array.forEach(function(currentValue, index, arr), thisValue)
	so idx parameter below represents index
	*/
    triangles.forEach((triangle, idx) => {
		
        var rotatedTriangle = triangle.map((point) => {
            point = point.rotateY(theta);//this was changed due to vector.js class
            point = point.rotateX(angle_mult * theta);//this was changed due to vector.js class - also adjusting angle_mult controls view of cube's top in rotation process
            return point;
        });
		
        //var color = colors[Math.floor(idx / 2)];
		var color = colors[Math.floor(idx/2)];
        renderTriangle(rotatedTriangle, color);
    });
    
	requestAnimationFrame(render);//this will call render function again
	//NOTE: requestAnimationFrame is js window doc function
	//see here: https://developer.mozilla.org/en-US/docs/Web/API/window/requestAnimationFrame
	//this function must be placed within the function calling it.
}

Let’s go over the main parts of render().

ctx is the context variable for canvas. ctx.fillStyle and ctx.fillRect() simply paint the background color of the canvas and produce its dimensions (the comment '//was black' is because I tested other background colors). And theta is the initial angle measurement, in radians, with dtheta the amount of change to produce the cube’s rotation animation in this program.


ctx.fillStyle = background_color;//was black
ctx.fillRect(0,0,W,H);
theta += dtheta;

Next, triangles.forEach() function is called.

A forEach() function is a JavaScript array function. The syntax for the forEach() function:

array.forEach(function(currentValue, index, arr), thisValue)

As stated on the w3schools website the forEach() method calls a function for each element in an array.

Here is an example: 


let myFunction = (a, b) => a * b;
document.getElementById("demo").innerHTML = myFunction(4, 5);
//answer: 20

One more thing. The JavaScript function map() needs to be discussed. As stated on the w3schools website about the map function , these are the main attributes of map():

  1. map() creates a new array from calling a function for every array element.
  2. map() calls a function once for each element in an array.
  3. map() does not execute the function for empty elements.
  4. map() does not change the original array.

Here is the triangles.forEach() function: 


triangles.forEach((triangle, idx) => {
		
    var rotatedTriangle = triangle.map((point) => {
        point = point.rotateY(theta);//this was changed due to vector.js class
        point = point.rotateX(angle_mult * theta);//this was changed due to vector.js class - also adjusting angle_mult controls view of cube's top in rotation process
        return point;
    });
		
    //var color = colors[Math.floor(idx)];
	var color = colors[Math.floor(idx/2)];
    renderTriangle(rotatedTriangle, color);
});

A summary of the code within triangles.forEach() up until the code return point:

return point;
  1. Recall that the function makeTriangle(a,b,c,dimension,side) uses five parameters but only returns [a,b,c] or [a,c,b]. So the array triangle will contain a group of x, y, and z points for each element in the array.
  2. triangles.forEach(triangle, idx) will take each group of 3D value (x, y, z) and alter them.
  3. Variable rotatedTriangle will be given each (x, y, z) point that was changed via point.rotateY(theta) and point.rotateX(angle_mult * theta). Please note that point in this instance is not a member of the points array, but merely a temporary variable. Both rotate functions are located within the vector.js class: 
    
    rotateY(theta){
	var x = this[0],
		y = this[1],
		z = this[2];
        
        return new Vector(
		Math.cos(theta)*x - Math.sin(theta)*z,//new x value
		y,//this is same y value as previous
		Math.sin(theta)*x + Math.cos(theta)*z//new z value
        );	
    }
    
    rotateX(theta){
	var x = this[0],
		y = this[1],
		z = this[2];
        return new Vector(
            x,
            Math.cos(theta)*y + Math.sin(theta)*z,//new y value
            -Math.sin(theta)*y + Math.cos(theta)*z//new z value
        );
    }
  4. Once rotateTriangle contains the altered 3D values (x, y, z) it can now be used in the next function call in render().

Now, two more lines of code need to be addressed that are yet within the triangles.forEach() function. 


//var color = colors[Math.floor(idx)];
var color = colors[Math.floor(idx/2)];
renderTriangle(rotatedTriangle, color);

Recall there is a colors array coded in the beginning of this program, in the global variables section.

What Math.floor(idx/2) does is described here at w3schools. "The Math.floor() method rounds a number DOWNWARDS to the nearest integer, and returns the result."

If you notice, idx is the index value in triangles.forEach((triangle, idx). Consequently idx/2 is taking the index of the current triangles array accessed in this function to get an index number for the colors array. By using the Math.floor() method this will insure that two of the triangles have the same index number and thus the same color. For example, if idx = 0 then 0/2 = 0 and if idx = 1 then 1/2 = 0 also. This is important so that each side of the cube will have the same color. The variable color will then hold this particular color.

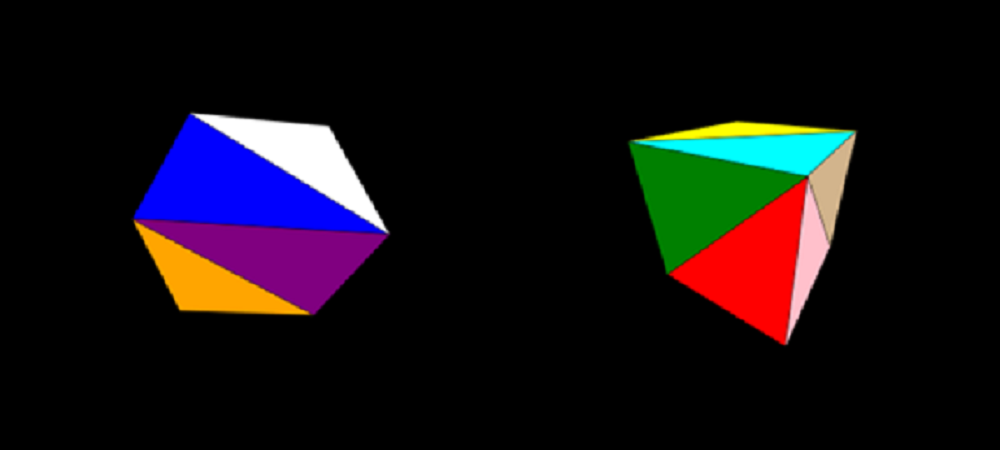
For experiment's sake, I tested idx alone, without being divided by 2. The rotating cube screen shots below show what occurred (but keep in mind I added more colors to the color array for a total of 12 colors):

renderTriangle(rotatedTriangle, color) will now get us where we really want to be – showing the moving triangle on the canvas, though keep in mind requestAnimationFrame(render) is in reality the main function that accomplishes all of this due to its constant repetition of the entire program. To learn more about function requestAnimationFrame() please visit this Mozilla page (also keep in mind that render must be the parameter in the function: requestAnimationFrame(render)).

In function renderTriangle() the 3D points of each corner of the cube are systematically transformed into 2D points while at the same time certain code is used to determine if each colored triangle on the cube should be seen or not. 


function renderTriangle(triangle, color){
	/*
	triangle.map(project) calls function project for each of the points in the triangle.
	function project will return x,y,z values that have been altered to fit on the 2D canvas, but the z value will NOT be used. 
	*/
    var projectedTriangle = triangle.map(project);
    var a = projectedTriangle[0],
        b = projectedTriangle[1],
        c = projectedTriangle[2];
		
    var side1 = b.subtract(a),
        side2 = c.subtract(b);

	//originally, if true, side gets drawn: if(side1.ccw(side2))
	//BUT dionyziz made an error in the Vector cross product function
	//so to adjust for this, if statement needs to be false
	//(if side1.ccw(side2) is altered to false by ! )
    if(!side1.ccw(side2)){
	
        //to draw triangles just need 2d points, hence only [0] and [1] for x and y
        ctx.beginPath();
        ctx.moveTo(a[0], a[1]);//start at 'a'
        ctx.lineTo(b[0], b[1]);
        ctx.lineTo(c[0], c[1]);
        ctx.lineTo(a[0], a[1]);//back to 'a'
        //ctx.strokeStyle = 'black';
		ctx.strokeStyle = 'black';
        ctx.fillStyle = color; 
        ctx.stroke();
        ctx.fill();
    } 
}

Here are the steps involved in function renderTriangle():

  1. renderTriangle(triangle, color) gets as inputs a triangle(three x, y, and z points) and a color.
  2. First thing in this function is variable projectedTriangle will receive a new triangle after triangle.map(project) is completed.
  3. In function project: 
    
//This function, along with the above function perspectiveProjection(point) takes 3D model coordinates and transforms them to 2D canvas coordinates.
function project(point){
	
	var perspectivePoint = perspectiveProjection(point);
	
	var x = perspectivePoint[0],
		y = perspectivePoint[1],
        z = perspectivePoint[2];//this was added for vector.js 
		
	//this code below positions the x,y points on the 2 canvas via actual pixel values
    return new Vector(
        W*(x - MODEL_MIN_X)/(MODEL_MAX_X - MODEL_MIN_X),
		H*(1 - (y - MODEL_MIN_Y)/(MODEL_MAX_Y - MODEL_MIN_Y)),
        z //z is needed to fulfill 3rd element in Vector BUT WILL NOT BE USED
    );	
}
    the variable perspectivePoint gets a 3D point from perspectiveProjection(point). Note that this section of the code:
    
	W*(x - MODEL_MIN_X)/(MODEL_MAX_X - MODEL_MIN_X),
	H*(1 - (y - MODEL_MIN_Y)/(MODEL_MAX_Y - MODEL_MIN_Y)),
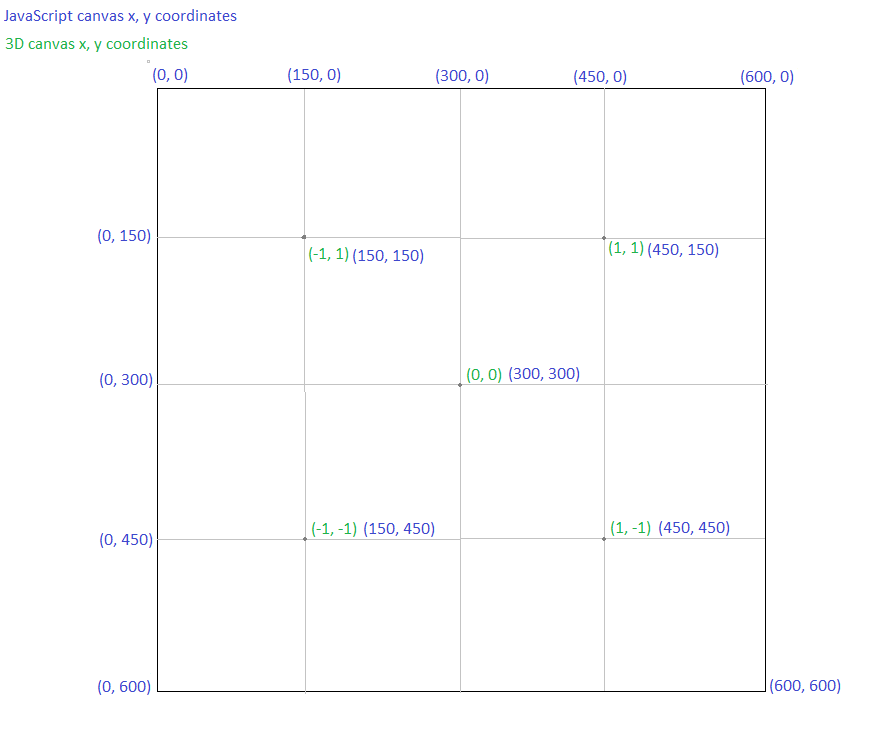
    is simply determining the position of x and the position of y by calculations based on the canvas height and width and a middle oriented origin location. JavaScript's canvas places the origin for the x, y axes at the top left corner of the canvas. Consequently, the origin needs to be "moved", so to speak, to the center of the canvas. So, 1/2*canvas_width and 1/2*canvas_height will correct for this (although in dionyziz's code this is not readily apparent at first sight, but it is still accomplished). Then, any x value to the left of the origin must be negated and similarly any y value below the origin. The calculations in the code will accomplish this. See the example and the accompanying image below for guidance.

    Example of (-1,-1):

    W*(x - MODEL_MIN_X)/(MODEL_MAX_X - MODEL_MIN_X)
    = 600*(-1 - (-2))/(2 - (-2))
    = 600*(1/4)
    = 150

    H*(1 - (y - MODEL_MIN_Y)/(MODEL_MAX_Y - MODEL_MIN_Y))
    = 600*(1 - (-1 - (-2))/(2 - (-2))
    = 600*(1 - (1)/(4)) = 600*3/4
    = 450

  4. Now, we got a little bit ahead of ourselves here but I wanted to make sure an adequate explanation for the conversion of the origin from points 3D to 2D was rather apparent. But obviously, variable perspectivePoint needs to be addressed, since it receives a return from function perspectivePoint(point).

    Within function perspectiveProjection(), the x, y values are altered by x/(z + view_distance) and y/(z + view_distance), where view_distance is a global variable and currently set to 3. An explanation for the mathematics behind this can be found here. A larger number will make the rotating cube seem farther away. 

    
//This function is supposed to return 2 values but returns 3 because 
//Vector class has three elements.
function perspectiveProjection(point){
	var x = point[0],
		y = point[1],
		z = point[2];

    return new Vector(//view_distance 
        x / (z + view_distance),//was z + 4
        y / (z + view_distance),
        z //original z value returned since Vector class has 3 elements
    );
}

    Also dionyziz drew an explanation in his video about the mathematics behind x/(z + view_distance) and y/(z + view_distance). I took a screen shot of the image and then added an example too in the image.

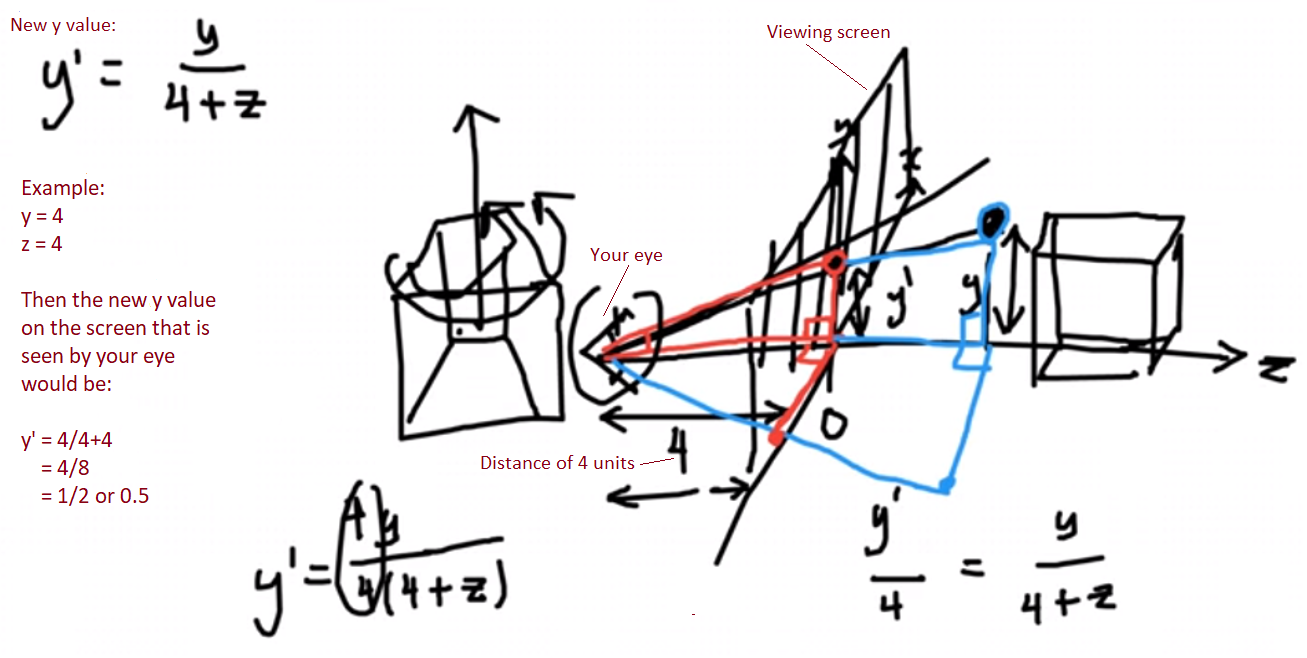
    But here are some typed examples too.

    If view_distance = 4, with y = 4 and z = 4, then the new y value on the screen that is seen by your eye would be:

    y' = 4/(4 + 4)
    = 4/8
    = 1/2 or 0.5

    If view_distance = 3, with y = 4 and z = 4:

    y' = 4/(4 + 3)
    = 4/7 or 0.57

    If view_distance = 2, with y = 4 and z = 4:

    y' = 4/(2 + 4)
    = 4/(6)
    = 2/3 or 0.67

    I would suggest playing around with the numbers. For instance see what x would be too, with a few trial numbers. Maybe even run some test code with a for loop, doing some x, y, z and view_distance variations and print the output with console.log().

  5. After receiving the x, y, z point from function perspectiveProjection(), each of the x, y, and z values within perspectivePoint are segregated. Keep in mind z is not used for the 2D rendering of the point but is used as a place-keeper for the three elements in the Vector class. 
    
var x = perspectivePoint[0],
y = perspectivePoint[1],
z = perspectivePoint[2];//this was added for vector.js
  6. Then next, side1 and side2 are obtained. By subtracting a from b and b from c, two vectors are created which are needed in the cross product calculation to determine which side of the cube needs to be colored. 
    
var side1 = b.subtract(a),
    side2 = c.subtract(b);
	
	//originally, if true, side gets drawn: if(side1.ccw(side2))
	//BUT dionyziz made an error in the Vector cross product function
	//so to adjust for this, if statement needs to be false
	//(if side1.ccw(side2) is altered to false by ! )
    if(!side1.ccw(side2)){
	
        //to draw triangles just need 2d points, hence only [0] and [1] for x and y
        ctx.beginPath();
        ctx.moveTo(a[0], a[1]);//start at 'a'
        ctx.lineTo(b[0], b[1]);
        ctx.lineTo(c[0], c[1]);
        ctx.lineTo(a[0], a[1]);//back to 'a'
        //ctx.strokeStyle = 'black';
		ctx.strokeStyle = 'black';
        ctx.fillStyle = color; 
        ctx.stroke();
        ctx.fill();
    }
    Once vectors side1 and side2 are obtained, function ccw(other), a Vector class function, is used to find if(!side1.ccw(side2)): 
    
cross(other){
    return new Vector(
        this[1] * other[2] - this[2] * other[1],
        this[0] * other[2] - this[2] * other[0],
	    //this[2]*other[0] - this[0]*other[2],
        this[0] * other[1] - this[1] * other[0]
    );
}
    
//this function determines if orientation is clockwise or counterclockwise for figuring out if camera (our eye) can see triangle or not
ccw(other){
    return this.cross(other)[2] > 0; //checks to see if z is positive or not, because if it's negative, we cannot see it then
}
    As mentioned earlier, dionyziz made an error in his cross(other) function in the Vector class file and so he had to compensate by changing if(side1.ccw(side2)) to if(!side1.ccw(side2)) I am not exactly sure why, though I see that the cross(other) method is different than the typical cross product setup, as can be seen here in code for the cross product in my matrix vector 2D 3D calculator:
    vx = y1*z2 - z1*y2;
    vy = z1*x2 - x1*z2;
    vz = x1*y2 - y1*x2;

    x1 = this[0]
    y1 = this[1]
    z1 = this[2]
    x2 = other[0]
    y2 = other[1]
    z2 = other[2]

    I ran some console.log() functions in various spots, to see what the numbers would look like. Take a gander at the few below. Interestingly, I noticed that whenever side1.ccw(side2) was false, the outputs came in twos, with two false outputs one right after the other. Note that these are in order from top left to right on down, like when reading:

    perspectivePoint = (-0.1987087405497928, -0.6773773082796274, -1.0646686215271028)
    perspectivePoint = (-0.2687701699197054, 0.43637079387281774, -1.5691594387958587)
    perspectivePoint = (-0.3754912203294132, -0.24022279201624716, 0.6243770315980792)
    a = (270.1936889175311, 401.60659624194415, -1.0646686215271028)
    b = (259.6844745120442, 234.54438091907733, -1.5691594387958587)
    c = (243.67631695058802, 336.0334188024371, 0.6243770315980792)
    side1 = (-10.509214405486944, -167.06221532286682, -0.5044908172687559)
    side2 = (-16.00815756145616, 101.48903788335977, 2.193536470393938)
    side1.ccw(side2) = false
    In if since side1.ccw(side2) = false    		 perspectivePoint = (-0.4362087784734207, 0.3412523881919753, 0.11988621432932317)
    perspectivePoint = (-0.3754912203294132, -0.24022279201624716, 0.6243770315980792)
    perspectivePoint = (-0.2687701699197054, 0.43637079387281774, -1.5691594387958587)
    a = (234.56868322898688, 248.8121417712037, 0.11988621432932317)
    b = (243.67631695058802, 336.0334188024371, 0.6243770315980792)
    c = (259.6844745120442, 234.54438091907733, -1.5691594387958587)
    side1 = (9.107633721601132, 87.2212770312334, 0.5044908172687561)
    side2 = (16.00815756145616, -101.48903788335977, -2.193536470393938)
    side1.ccw(side2) = false
    In if since side1.ccw(side2) = false
    perspectivePoint = (0.4725236069837249, -0.36966199975296415, -0.11988621432932317)
    perspectivePoint = (0.08416586593533083, -0.1366503051516682, 1.5691594387958587)
    perspectivePoint = (0.5728694210445985, 0.36649669641632543, -0.6243770315980792)
    a = (370.8785410475587, 355.4492999629446, -0.11988621432932317)
    b = (312.62487989029967, 320.49754577275024, 1.5691594387958587)
    c = (385.9304131566898, 245.02549553755122, -0.6243770315980792)
    side1 = (-58.253661157259046, -34.95175419019438, 1.6890456531251818)
    side2 = (73.30553326639011, -75.47205023519902, -2.193536470393938)
    side1.ccw(side2) = true    		 perspectivePoint = (0.09461220497191754, 0.32252310873168943, 1.0646686215271028)
    perspectivePoint = (0.5728694210445985, 0.36649669641632543, -0.6243770315980792)
    perspectivePoint = (0.08416586593533083, -0.1366503051516682, 1.5691594387958587)
    a = (314.1918307457876, 251.6215336902466, 1.0646686215271028)
    b = (385.9304131566898, 245.02549553755122, -0.6243770315980792)
    c = (312.62487989029967, 320.49754577275024, 1.5691594387958587)
    side1 = (71.73858241090215, -6.596038152695371, -1.689045653125182)
    side2 = (-73.30553326639011, 75.47205023519902, 2.193536470393938)
    side1.ccw(side2) = true
    perspectivePoint = (-0.1987087405497928, -0.6773773082796274, -1.0646686215271028)
    perspectivePoint = (-0.3754912203294132, -0.24022279201624716, 0.6243770315980792)
    perspectivePoint = (0.4725236069837249, -0.36966199975296415, -0.11988621432932317)
    a = (270.1936889175311, 401.60659624194415, -1.0646686215271028)
    b = (243.67631695058802, 336.0334188024371, 0.6243770315980792)
    c = (370.8785410475587, 355.4492999629446, -0.11988621432932317)
    side1 = (-26.517371966943102, -65.57317743950705, 1.689045653125182)
    side2 = (127.2022240969707, 19.415881160507524, -0.7442632459274023)
    side1.ccw(side2) = true    		 perspectivePoint = (0.08416586593533083, -0.1366503051516682, 1.5691594387958587)
    perspectivePoint = (0.4725236069837249, -0.36966199975296415, -0.11988621432932317)
    perspectivePoint = (-0.3754912203294132, -0.24022279201624716, 0.6243770315980792)
    a = (312.62487989029967, 320.49754577275024, 1.5691594387958587)
    b = (370.8785410475587, 355.4492999629446, -0.11988621432932317)
    c = (243.67631695058802, 336.0334188024371, 0.6243770315980792)
    side1 = (58.253661157259046, 34.95175419019438, -1.6890456531251818)
    side2 = (-127.2022240969707, -19.415881160507524, 0.7442632459274023)
    side1.ccw(side2) = true

  7. Finally, if side1.ccw(side2) is false, the triangle can be drawn (and note in the comment, like discussed earlier, that the code is such because of the cross product error). 

    
//originally, if true, side gets drawn: if(side1.ccw(side2))
//BUT dionyziz made an error in the Vector cross product function
//so to adjust for this, if statement needs to be false
//(if side1.ccw(side2) is altered to false by ! )
if(!side1.ccw(side2)){
	
    //to draw triangles just need 2d points, hence only [0] and [1] for x and y
    ctx.beginPath();
    ctx.moveTo(a[0], a[1]);//start at 'a'
    ctx.lineTo(b[0], b[1]);
    ctx.lineTo(c[0], c[1]);
    ctx.lineTo(a[0], a[1]);//back to 'a'
    //ctx.strokeStyle = 'black';
	ctx.strokeStyle = 'black';
    ctx.fillStyle = color; 
    ctx.stroke();
    ctx.fill();
}
    Only a[0], a[1] are used, and similarly for b and c, because a[2] is the z element but is NOT included in 2D rendering, as mentioned above. z is certainly used in the calculation for x and y, with the x/(z+ view_distance) and y/(z + view_distance) code, but z itself is not graphed in a 2D canvas context.

And so now, all that has to be done is for requestAnimationFrame(render) 


requestAnimationFrame(render);//this will call render function again
to call the render() function continuously. But though requestAnimationFrame(render) is called repeatedly, the code theta += dtheta, seen below 

function render(){
	ctx.fillStyle = background_color;//was black
	ctx.fillRect(0,0,W,H);
	theta += dtheta;
as well as the functions in vector.js 

rotateY(theta){
	var x = this[0],
		y = this[1],
		z = this[2];
        
        return new Vector(
		Math.cos(theta)*x - Math.sin(theta)*z,//new x value
		y,//this is same y value as previous
		Math.sin(theta)*x + Math.cos(theta)*z//new z value
        );	
    }
    
    rotateX(theta){
	var x = this[0],
		y = this[1],
		z = this[2];
        return new Vector(
            x,
            Math.cos(theta)*y + Math.sin(theta)*z,//new y value
            -Math.sin(theta)*y + Math.cos(theta)*z//new z value
        );
    }
are the main components for getting the cube in motion, because of the continuously changing angle number.

To learn more about using canvas functions to draw lines, shapes, and fill background colors, please visit the w3schools canvas tutorial.

That will conclude this blog. Thank you for visiting and reading :-)

Below, I have listed cube2_2.js and vector.js. Since I was hectically typing in both code and comments while watching dionyziz's video for this program, I removed or edited many of my original comments in these two files to make the code easier to see and read. If you have any questions or comments, please contact me at dcwendeavors@gmail.com.

cube2_2.js


//cube2_2.js file

/* GLOBAL VARIABLES */
var W = 600, H = 600; //variables for size of canvas
var STEP = 0.3;//original one is 0.5
var perspective_distance = 3.5;//was 2.5
var MODEL_MIN_X = -2, MODEL_MAX_X = 2;
var MODEL_MIN_Y = -2, MODEL_MAX_Y = 2;
var canvas = document.getElementById('canvas');
var ctx = canvas.getContext('2d');
//view_distance - lower numbers closer, higher numbers farther away
var view_distance = 3; //used in perspectiveProjection(point), original value 4 - and larger number draws cube farther away

//angle values:
var theta = 0;//original value was 0
var dtheta = 0.01;//original value was 0.01 - note, 0.2 makes the cube spin rapidly
var background_color = 'black';
var angle_mult = 0.5;//original value 0.43 - appears to control if top of cube is shown during the rotation process

var points = []; //points array instantiation
var triangles = [];//triangle array to create sides of the box object
var colors = [
    'red', 'green', 'blue', 'white', 
    'orange', 'purple'
];//colors for each side of cube, 6 total sides

function makeTriangle(a,b,c,dimension,side){
    var side1 = b.subtract(a),
        side2 = c.subtract(a);
	console.log("side1 = "+side1.print()+" side2 = "+side2.print());
    var orientationVector = side1.cross(side2);
	
	//test code below - needs to be removed
	console.log("orientationVector = "+orientationVector.print());
	var testcross1 = Math.sign(orientationVector[dimension]);
	var testcross2 = Math.sign(side);
	console.log("Math.sign(orientationVector["+dimension+"]) = "+testcross1+" Math.sign(side) = "+testcross2);
	//end test code

    if(Math.sign(orientationVector[dimension]) == Math.sign(side)){
		console.log("return a,b,c "+a.print()+", "+b.print()+", "+c.print());
        return [a,b,c];
    }
	console.log("return a,c,b "+a.print()+", "+c.print()+", "+b.print());
    return [a,c,b];
}

function initGeometry(){
	//cube is only going to have -1 and 1 for each side, 
	//doesnt' need all the points like in the first cube
	for(var x = -1; x <= 1; x +=2){
		for(var y = -1; y <= 1; y +=2){
			for(var z = -1; z <= 1; z +=2){
				//points.push([x,y,z]);//was this, until he implemented vector.js for crossproduct functionality
				//NOTE - Vector is a class in vector.js file
				//console.log("x = "+x+" y = "+y+" z = "+z);
                points.push(new Vector(x,y,z));//vector.js is a class
			}
		}
	}
	//NOTE - THIS for loop below is what gets points for both neg pos sides of cube along each axis
	for(var dimension = 0; dimension <= 2; ++dimension){
		for(var side = -1; side <= 1; side += 2){
			//NOTE - filter is a js function for arrays
			console.log("dimension = "+dimension+" side = "+side);
			var sidePoints = points.filter((point) => {
				console.log("point["+dimension+"] == "+point[dimension]+" side = "+side);
				return point[dimension] == side;//return if point[dimension] is equal to side (but return is meant to return a value to sidePoints from points.filter() keep in mind, it does not return out of the current for loop or initGeometry)
			});
			//console.log("points["+dimension+"] = "+points[dimension]);
			//console.log("sidePoints["+dimension+"] = "+sidePoints[dimension]);
			var a = sidePoints[0], 
				b = sidePoints[1],
				c = sidePoints[2],
				d = sidePoints[3];
			//console.log("a = "+a.print()+" b = "+b.print()+" c = "+c.print()+" d = "+d.print());
            
            if(dimension == 1){//he added this due to issues with y dimension, around 35:00 mark in video
			
				triangles.push(makeTriangle(a,b,c,dimension,side));
				triangles.push(makeTriangle(d,b,c,dimension,side));
            }else{
                triangles.push(makeTriangle(a,b,c,dimension,-side));
                triangles.push(makeTriangle(d,b,c,dimension,-side));//he said adding -side was needed because he made an error in his cross product function
            }
		}//end for loop for side
	}//end for loop for dimension
}

function perspectiveProjection(point){
	var x = point[0],
		y = point[1],
		z = point[2];

    return new Vector(//NOTE -> (z + number), number is the viewing distance
        x / (z + view_distance),//was z + 4
        y / (z + view_distance),
        z //he adds this since vector.js takes 3 things
        );
}

function project(point){//this function takes coordinates from the model space, which is the 3D space, and projects them into 2dimension space - this should also remove the z component because only x,y shows on 2D canvas
//so basically takes 3d point and makes it 2dimension
	var perspectivePoint = perspectiveProjection(point);
	var x = perspectivePoint[0],
		y = perspectivePoint[1],
        z = perspectivePoint[2];//this was added after he added vector.js to the return thing below
        
    /*
    //he did have this below, but then used vector.js instead, see below this commented out portion
	return [
		//this below takes from -2 to 2 and gives value of from 0 to min or max canvas dimensions
		W*(x - MODEL_MIN_X)/(MODEL_MAX_X - MODEL_MIN_X),
		H*(1 - (y - MODEL_MIN_Y)/(MODEL_MAX_Y - MODEL_MIN_Y))//1- added so to convert canvas y direction to 3d y direction (positive up)
	];*/
    
    return new Vector(
        W*(x - MODEL_MIN_X)/(MODEL_MAX_X - MODEL_MIN_X),
		H*(1 - (y - MODEL_MIN_Y)/(MODEL_MAX_Y - MODEL_MIN_Y)),
        z //he adds this since vector takes 3 things
    );
	
}

//this function is used by render() and 
//gets help from project(point)
function renderPoint(point){//this function takes a point and draws it
	var projectedPoint = project(point);
	var x = projectedPoint[0],
		y = projectedPoint[1];
	ctx.beginPath();
	ctx.moveTo(x,y);
	ctx.lineTo(x + 2, y + 2);//both these were 1
	ctx.lineWidth = 2;//this was 4
	ctx.strokeStyle = 'white';//this was white
	ctx.stroke();
	
}

function renderTriangle(triangle, color){
    /* map will call project to each of the points in the triangle, he said, and it will
    return the 1st,2nd,3rd point of each triangle
    to the projectedTriangle, a new triangle, each of 
    which has 3 points in it. 
    */    
	var projectedTriangle = triangle.map(project);
    var a = projectedTriangle[0],
        b = projectedTriangle[1],
        c = projectedTriangle[2];
	
    //this code below is to determine if we can see the side or not from our view, using ccw function in vector.js    
    var side1 = b.subtract(a),
        side2 = c.subtract(b);
    
    if(!side1.ccw(side2)){//if true, side gets drawn - its not actually correct, what he did, since he made an error in his crossproduct function, so he added ! to fix it
        
        //to draw them, just needs 2d canvas: 
        ctx.beginPath();
        //goes from a back to a to draw triangles completely
        ctx.moveTo(a[0], a[1]);//start at 'a'
        ctx.lineTo(b[0], b[1]);
        ctx.lineTo(c[0], c[1]);
        ctx.lineTo(a[0], a[1]);//back to 'a'
        ctx.strokeStyle = 'black';
        ctx.fillStyle = color; 
        ctx.stroke();
        ctx.fill();
    }  
}

function render(){
	ctx.fillStyle = background_color;//was black
	ctx.fillRect(0,0,W,H);
	//ctx.clearRect(0, 0, W, H);//x value, y value, width of canvas, height of canvas
	theta += dtheta;
 
    /*
    This is how triangles.forEach() works:
    triangles is an array and so 
    triangles.forEach is called for each of the triangles array elements. 
    It's passing the one triangle element, that is about to be drawn.
    Before it's rendered, needs to be rotated, and once
    rotated, it is passed to renderTriangle()
    */
    triangles.forEach((triangle, idx) => {
        //instead of rotating individual points, he will rotate all the points of the triangle
		//recall => js function sign: 
		/*
		example:
		let myFunction = (a, b) => a * b;
		document.getElementById("demo").innerHTML = myFunction(4, 5);
		answer: 20
		*/
        var rotatedTriangle = triangle.map((point) => {
            point = point.rotateY(theta);//this was changed due to vector.js class
            point = point.rotateX(angle_mult * theta);//this was changed due to vector.js class - also angle_mult causes top of cube to show more in rotation process
            return point;
        });
        /*
        For the idx parameter in forEach function, 
        triangle array is 0 up to 11, so he is going to
        divide by 2 on idx to get a number.
        He uses Math.floor(idx/2) so each side 
        will have one color. 
        */
        var color = colors[Math.floor(idx / 2)];
        renderTriangle(rotatedTriangle, color);
    });
    
	requestAnimationFrame(render);//this will call render function again
	//NOTE: requestAnimationFrame is js window doc function
	//see here: https://developer.mozilla.org/en-US/docs/Web/API/window/requestAnimationFrame
	//this function must be placed within the function calling it.
}

initGeometry();//called first
render(); //then this function is called

vector.js 


//vector.js file

class Vector{
    constructor(x,y,z){
        this[0] = x;
        this[1] = y;
        this[2] = z;
        
    }
	
	/*//from my cross product on 3d graphing 
	vx = y1*z2 - z1*y2;
	vy = z1*x2 - x1*z2;
	vz = x1*y2 - y1*x2;
	
	*/
    
    cross(other){
        return new Vector(
            this[1] * other[2] - this[2] * other[1],
            this[0] * other[2] - this[2] * other[0],
			//this[2]*other[0] - this[0]*other[2],
            this[0] * other[1] - this[1] * other[0]
        );
    }
    
    //this function determines if orientation is clockwise or counterclockwise for figuring out if camera (our eye) can see triangle or not
    ccw(other){
        return this.cross(other)[2] > 0; //checks to see if z is positive or not, because if its negative, we cannot see it then
    }
    
    add(other){
        return new Vector(
            this[0] + other[0],
            this[1] + other[1],
            this[2] + other[2]
        
        );
    }
    
    scale(scalar){
        return new Vector(
            this[0]*scalar,
            this[1]*scalar,
            this[2]*scalar
        );
        
    }
    
    subtract(other){
        /*
        return new Vector(
            this[0] - other[0],
            this[1] - other[1],
            this[2] - other[2]
        );*/
        return this.add(other.scale(-1));
    }
	
	//NOTE - print() was added by me so as to observe, via console.log() the contents of outputs
	print(){
		//return "this[0] = "+this[0]+" this[1] = "+this[1]+" this[2] = "+this[2];
		return "("+this[0]+", "+this[1]+", "+this[2]+")";
	}
    
    rotateY(theta){
	var x = this[0],
		y = this[1],
		z = this[2];
        
        return new Vector(
		Math.cos(theta)*x - Math.sin(theta)*z,//this is new x value
		y,//this is same y value as previous
		Math.sin(theta)*x + Math.cos(theta)*z//this is the new z value
        );	
    }
    
    rotateX(theta){
	var x = this[0],
		y = this[1],
		z = this[2];
        return new Vector(
            x,//original x
            Math.cos(theta)*y + Math.sin(theta)*z,//this is new y value
            -Math.sin(theta)*y + Math.cos(theta)*z//this is the new z value
        );
    }
}